Computing Melting Point by Free Energy Method

Computing Melting Point by Free Eneregy Method

Seunghwa Ryu and Wei Cai

Modified by Yanming Wang (Sep 2015)

This tutorial describes how to compute melting points from free energy methods. We provide the MD++ script files and describe how to use them in detail. The theoretical background is published in

Comparison of Thermal Properties Predicted by Interatomic Potential Models, Modelling and Simulation in Materials Science and Engineering, 16, 085005 (2008). (PDF) (Paper selected as MSMSE featured article).

This case study is also available in the form of a Python jupyter notebook.

Download files

First, you need to install MD++ on your computer by following the instructions on MD++ Manuals.

Second, copy files melting_cubic.tcl and melting_noncubic.tcl to your input file directory of MD++. You can do so by the following commands (assuming you have installed MD++ in ~/Codes/MD++).

 export MDPP=~/Codes/MD++
 mkdir -p ${MDPP}/scripts/work/melting
 cd ${MDPP}/scripts/work/melting
 wget http://micro.stanford.edu/mediawiki-1.11.0/images/Melting_cubic.tcl.txt -O melting_cubic.tcl
 wget http://micro.stanford.edu/mediawiki-1.11.0/images/Melting_noncubic.tcl.txt -O melting_noncubic.tcl

Both files contain a big comment section in the beginning that describes in detail the (16) steps to compute the melting point. These steps are fully automated. In this tutorial, we describe how to run these scripts on a parallel cluster (using wcr.stanford.edu as an example) and what kind of results you should expect.

Compile executable file

Different executables in MD++ contains different interatomic potentials, for example,

sw                  - Stillinger-Weber Silicon (modified by Balamane et al.)
sworig              - Original version of SW Silicon
swge                - Stillinger-Weber Germanium
tersoff             - Tersoff potential for Silicon
meam-lammps         - MEAM (taken from lammps)
meam-baskes         - MEAM (taken from Baskes's code dynamo)
meam                - MEAM (directly implemented in MD++)
eam                 - Embedded Atom Method 
fs                  - Finnis-Sinclair

Here we use Si as an example. You can compile sworig by typing

 cd ${MDPP}
 make sworig build=R SYS=wcr

If compilation is successful, this will create binary file sworig_wcr file in your ${MDPP}/bin directory.

The script melting_cubic.tcl can be used with many potentials (i.e. executables), which are explained in the header region of the file. Contact shryu@stanford.edu if you have further questions.

Submit jobs

Here are the PBS scripts (melt1.pbs and melt2.pbs) for submitting the jobs on wcr.stanford.edu. You can submit jobs by typing the following commands. This is a test case that computes the melting points of silicon described by the Stillinger-Weber (SW) potential on the parallel cluster wcr.stanford.edu.

 cd ${MDPP}
 mkdir runs/Single_Elem_Tm
 wget http://micro.stanford.edu/mediawiki-1.11.0/images/Melt1.pbs.txt -O melt1.pbs
 wget http://micro.stanford.edu/mediawiki-1.11.0/images/Melt2.pbs.txt -O melt2.pbs
 qsub melt1.pbs
 qsub melt2.pbs

After the calculation is finished (within 24 hours), the free energy data will be stored in the following two directories.

${MDPP}/runs/Single_Elem_Tm/SW_Si_Solid/
${MDPP}/runs/Single_Elem_Tm/SW_Si_Liquid/

Analyse data

At the end of the calculation, data files and Matlab files will be automatically generated. Transfer these files to a location where you have Matlab installed. Run the following commands in Matlab and you will get the free energy plot (for solid and liquid phases). The melting point is the temperature at which the two free energy curves cross.

In this test case, the analysis files are generated in directory ${MDPP}/runs/Single_Elem_Tm. They are

Hessian_SW_Si.m
Free_Energy_of_SW_Si.m
tar_SW_Si

Run the following command to zip all data

 cd ${MDPP}/runs/Single_Elem_Tm
 ./tar_SW_Si

into a tar file inter_SW_Si.tar.

Copy this file to your local computer and unzip the data. Next, run the following command in Matlab.

Hessian_SW_Si.m
Free_Energy_of_SW_Si.m

You'll see the following output files that contain all free energy data and the error analysis.

Solid Free Energy Info

lattice const =    5.43095
strain =    0.00518
E_0 = -2218.74337 eV (   -4.33348 eV/atom)
F_w = -253.34582 eV (   -0.49482 eV/atom)
F_ha = E_0 + F_w = -2472.08919 eV (   -4.82830 eV/atom)
W_re_to_ha =    5.99169 eV (    0.01170 eV/atom)
W_ha_to_re =   -7.30068 eV (   -0.01426 eV/atom)
F_re - F_ha = (W_ha_to_re - W_re_to_ha)/2 =   -6.64619 eV (   -0.01298 eV/atom)
F_re at 1600.000000 = -2478.73538 eV (   -4.84128 eV/atom)
W_T1_to_T11 =  417.87095 eV (    0.81615 eV/atom)
W_T11_to_T1 = -417.87508 eV (   -0.81616 eV/atom)
dW1 = (W_T1_to_T11 - W_T11_to_T1)/2 =  417.87302 eV (    0.81616 eV/atom)
F_re at 2000.000000 = -2605.55266 eV (   -5.08897 eV/atom)

Liquid Free Energy Info

strain =   -0.01894
F_ideal = -919.36940 (   -1.79564 eV/atom)
W_re_to_ga = 1888.21102 eV (    3.68791 eV/atom)
W_ga_to_re = -1887.53306 eV (   -3.68659 eV/atom)
F_re - F_ga = (W_ga_to_re - W_re_to_ga)/2 = -1887.87204 eV (   -3.68725 eV/atom)
W_ga_to_id = -256.29295 eV (   -0.50057 eV/atom)
W_id_to_ga =  256.52177 eV (    0.50102 eV/atom)
F_ga - F_id = (W_id_to_ga - W_ga_to_id)/2 =  256.40736 eV (    0.50080 eV/atom)
F_re at 1800.000000 = -2550.83408 eV (   -4.98210 eV/atom)
W_T2_to_T22 = -583.02785 eV (   -1.13873 eV/atom)
W_T22_to_T2 =  583.06542 eV (    1.13880 eV/atom)
dW2 = (W_T2_to_T22 - W_T22_to_T2)/2 = -583.04664 eV (   -1.13876 eV/atom)
F_re at 1384.615385 = -2386.68534 eV (   -4.66149 eV/atom)

Error Analysis

Solid Side
Err_re_to_ha =    0.02769 eV ( 0.00005407 eV/atom)( 0.628 K)
Err_ha_to_re =    0.02815 eV ( 0.00005498 eV/atom)( 0.638 K)
Err_T1_to_T11 =    0.00374 eV ( 0.00000730 eV/atom)( 0.085 K)
Err_T11_to_T1 =    0.00441 eV ( 0.00000861 eV/atom)( 0.100 K)

Liquid Side
Err_re_to_ga =    0.04793 eV ( 0.00009362 eV/atom)( 1.086 K)
Err_ga_to_re =    0.06601 eV ( 0.00012893 eV/atom)( 1.496 K)
Err_ga_to_id =    0.02557 eV ( 0.00004993 eV/atom)( 0.580 K)
Err_id_to_ga =    0.03421 eV ( 0.00006682 eV/atom)( 0.776 K)
Err_T2_to_T22 =    0.01488 eV ( 0.00002906 eV/atom)( 0.337 K)
Err_T22_to_T2 =    0.01183 eV ( 0.00002311 eV/atom)( 0.268 K)
Max dT =  2.315
Tm= 1695.08000 (K), err= 1.044 Fm =   -4.89779 (eV/atom)
L=      165.8833097832 (eV) Ss=0.308452 Sl=0.406313
L=        0.3239908394 (eV/atom) ss=0.000602 sl=0.000794
L=    31206.7976529696 (J/mol) ss=58.027496 sl=76.437718
L=  1111115.7748689589 (J/kg) ss=2066.064819 sl=2721.559412

The Gibbs free energy (in eV/atom) as a function of temperature (in K) of the solid (blue) and liquid (green) phases of silicon described by the Stillinger-Weber (SW) potential. The intersection of the two curves determines the melting point.

Melting point of Other Elements

MEAM Si

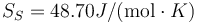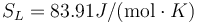Following the same procedure, we can evaluate the melting point of Au with the meam-lammps potential. The results are $T m = 1140.1$ K, $L = 1315 J / g$ , $S_S = 48.70 J/(\mbox{mol}\cdot K)$ and $S_L = 83.91 J/(\mbox{mol}\cdot K)$ .

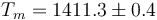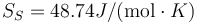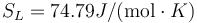The above results are in good agreement with MSMSE 16, 085005 (2008), Table 1, in which $T_m = 1411.3 \pm 0.4$ K, $L = 1309 J / g$ , $S_S = 48.74 J/(\mbox{mol}\cdot K)$ and $S_L = 74.79 J/(\mbox{mol}\cdot K)$ .

MEAM Au

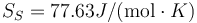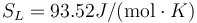Following the same procedure, we can evaluate the melting point of Au with the meam-lammps potential. The results are $T m = 1145$ K, $L = 92.4 J / g$ , $S_S = 77.63 J/(\mbox{mol}\cdot K)$ and $S_L = 93.52 J/(\mbox{mol}\cdot K)$ .

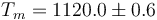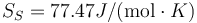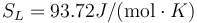This is to be compared with MSMSE 16, 085005 (2008), Table 1, in which $T_m = 1120.0 \pm 0.6$ K, $L = 92 J / g$ , $S_S = 77.47 J/(\mbox{mol}\cdot K)$ and $S_L = 93.72 J/(\mbox{mol}\cdot K)$ .

The agreement on $L$ , $S S$ , and $S L$ is pretty good. The values of $T m$ do not agree so well.

EAM Au

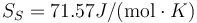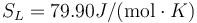Following the same procedure, we can evaluate the melting point of Cu with the eam potential. The results are $T m = 1229.6$ K, $L = 161 J / g$ , $S_S = 71.57 J/(\mbox{mol}\cdot K)$ and $S_L = 79.90 J/(\mbox{mol}\cdot K)$ .

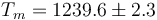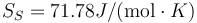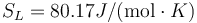This is to be compared with MSMSE 16, 085005 (2008), Table 1, in which $T_m = 1239.6 \pm 2.3$ K, $L = 164 J / g$ , $S_S = 71.78 J/(\mbox{mol}\cdot K)$ and $S_L = 80.17 J/(\mbox{mol}\cdot K)$ .

The relative differences in $T m$ , $L$ , $S S$ , and $S L$ are all around or less 1%.

MEAM Ge

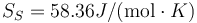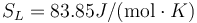Following the same procedure, we can evaluate the melting point of Au with the meam-lammps potential. The results are $T m = 1216.5$ K, $L = 426.8 J / g$ , $S_S = 58.36 J/(\mbox{mol}\cdot K)$ and $S_L = 83.85 J/(\mbox{mol}\cdot K)$ .

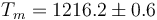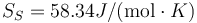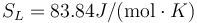This is to be compared with MSMSE 16, 085005 (2008), Table 1, in which $T_m = 1216.2 \pm 0.6$ K, $L = 427 J / g$ , $S_S = 58.34 J/(\mbox{mol}\cdot K)$ and $S_L = 83.84 J/(\mbox{mol}\cdot K)$ .

The agreement is fantastic

SW Ge

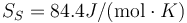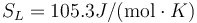Following the same procedure, we can evaluate the melting point of Au with the meam-lammps potential. The results are $T m = 2902.1$ K, $L = 836.3 J / g$ , $S_S = 84.4 J/(\mbox{mol}\cdot K)$ and $S_L = 105.3 J/(\mbox{mol}\cdot K)$ .

This is to be compared with MSMSE 16, 085005 (2008), Table 1, in which 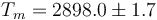$T_m = 2898.0 \pm 1.7$ K, $L = 847 J / g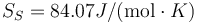$ , $S_S = 84.07 J/(\mbox{mol}\cdot K)$ and $S_L = 105.30 J/(\mbox{mol}\cdot K)$ .

The agreement is OK, not too outside the error bar.

Contents