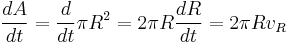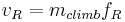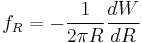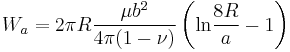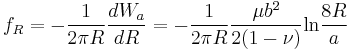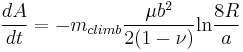Micro and Nano Mechanics Group

Prismatic Loop

The Burgers vector of a prismatic dislocation loop is perpendicular to the plane of the dislocation loop. If such a dislocation loop moves across a solid through glide, the material that is displaced will look like a prism with the shape of the dislocation loop as its cross-section. In the absence of any external stress, a prismatic loop shrinks through climb. From an energetic point of view, the existence of a dislocation loop requires energy and a dislocation loop shrinks to minimize the total energy of the system. Let us investigate the rate of change of area of a prismatic loop in the absence of external stresses.

Energy and Kinetics of a Circular Prismatic Loop

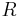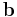Consider a circular prismatic loop with radius R \, and Burgers vector \mathbf{b}. The rate of change of area of the circular loop with respect to time t is 

\frac{dA}{dt}=\frac{d}{dt}\pi R^2=2\pi R\frac{dR}{dt}=2\pi Rv_R

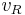where v_R \, is the magnitude of the radial velocity for the points or line segments that constitute the loop. In our nodal representation of dislocation lines, the velocity of the nodes is calculated using a linear mobility law 

v_R = m_{climb}f_R\,

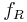where f_R \, is the force per unit length experienced by a dislocation node on the loop and 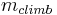m_{climb}\, the climb mobility of an edge dislocation. If we let 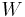W\,be self-energy of a dislocation loop, the force per unit length on each node is given by 

f_R=-\frac{1}{2\pi R}\frac{dW}{dR}

In the non-singular continuum formalism of Cai W et. al. the self-energy of a dislocation loop 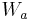W_a \, is given by 

W_a = 2\pi R\frac{\mu b^2}{4\pi (1-\nu)}\left(\mathrm{ln}\frac{8R}{a}-1\right)

So the force per unit length within this formalism is given by 

 f_R=-\frac{1}{2\pi R}\frac{dW_a}{dR}=-\frac{1}{2\pi R} \frac{\mu b^2}{2(1-\nu)}\mathrm{ln}\frac{8R}{a}

Therefore the rate of change of area of a circular dislocation loop in the non-singular continuum formalism can be written as 

\frac{dA}{dt}=-m_{climb}\frac{\mu b^2}{2(1-\nu)}\mathrm{ln}\frac{8R}{a}


Comparision with DDLab simulations

Here we will put some matlab plots.

First, loop area versus time. For different lmin = 10, 50, 100. Initial R = 500.

Second, radius versus time.

We would like to get analytic solution of R(t) (e.g. from Maple) and compare with DD simulation.

What is the purpose of this comparison?

1. The nodal speed and the total life time of the loop

2. What is the accuracy of approximating the area of a circle by a polygon.

How can we calculate the radius of the polygon?

Retrieved from "http://micro.stanford.edu/mediawiki/index.php?title=Test_Case:_Dislocation_Loop&oldid=700"
Member Login