Contents 1 Introduction 2 Input parameters of DDLab 3 Nodal representation of dislocation structure 4 Mobility 5 Integrator 6 Topological Changes 7 Time controls 8 Display controls 9 Materials constants 10 Miscellaneous 10.1 Flow of the code in DDLab 10.2 Subroutines details 10.3 Integrator 10.4 Self consistency in DDLab units

Introduction

The purpose of this document is to give a brief description of DDLab. If advanced users are interested in the algorithms of the code, they may simply look at the source code. We have tried to write and organize the subroutines in a compact yet readable manner.

Warning: The main executable file dd3d.m requires the compilation of

 mex -O SegSegForces.c

You need to have a C compiler installed on your computer to make it work. This is ok when you use gcc-3.3. You may have difficulty compiling with higher version of gcc.

Input parameters of DDLab

There are various input parameters in DDLab. In this section, we don't give a detailed expla- nation of each parameter but we explain some. The relation between parameters will be explained in more detail in the following sections.

We can divide all input parameters into the following categories.

• Dislocation structure : rn, links* Mobility : mobility
• Integrator : integrator
• Topological changes : lmax, lmin, areamin, areamax, rmax, rann, rntol, doremesh, docollision, desepraration
• Time controls : totalstpes, dt0
• Display controls : plotfreq, plim, viewangle, printfreq, printnode
• Materials constant : MU (shear modulus), NU (Poisson's ratio), Ec (core energy), a (core radius)
• Miscellaneous : appliedstress, maxconnections

Nodal representation of dislocation structure

Figure 1: Nodal representation of dislocation structure Fig. 1 shows a simple approach that can represent an arbitrary dislocation network. The dislocations are specified by a set of nodes that are connected with each other by straight segments. Each segment has a nonzero Burgers vector. Because the Burgers vector is defined only after a sense of direction is chosen for the dislocation line, we can define bij

Mobility

In DDLab, the motion of dislocation is expressed by the motion of nodes. Thus, mobility gives the velocity. DDLab contains several mobility laws; mobfcc1.m, mobfcc0.m, and mobbcc0.m.

Integrator

An integrator scheme is used to calculate the position of each nodes for a given time step. The nodal forces and mobility model comprise the equation motion for the nodes 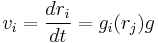where g_i sums up both the nodal force and the mobility model. This is a first ordinary differential equation and we solve it by integration. DDLab contains two numerical integrator: eulerforward.m, newtonkrylov.m. ode15s.m, trapezoid.m. In this work, we use trapezoid.m is used.

Topological Changes

In order to accurately represent dislocation behavir and also for numerical efficiency, we need a way to handle topological changes, i.e. changes in the connectivity of nodes. For example, should a line change its length and/or curvature during the simulation, it may become necessary to adjust the number of nodes used to represent this dislocation line. The following parameters are used for topological changes in DDLAB.

• lmax: Maximum length of a dislocation segment
• lmin: Minimum length of a dislocation segment
• areamin: Maximum area criterion
• areamax: Minimum area criterion
• rmax: maximum distance a node may travel in one cycle
• rann: annihilation distance used to calculate the collision of dislocation lines
• rntol: solution tolerance used to control the automatic timestepping
• doremesh: Toggle remesh.m for remeshing nodes. doremesh is set as zero to disable

 the use of remesh rule. When it is set as zero, it is enabled.

Time controls

The following parameters are for time controls.

• totalsteps : number of cycles that are run for completion of dd3d command
• dt0 : largest timestep that can be taken during a cycle

Display controls

The following parameters are for display controls

• plotfreq : number of cycles between monitored node write statements
• plim : limits of plotting space
• viewangle : angle of viewpoint for the 3D plot of the geometry
• printfreq : number of cycles between monitored node write statements
• printnode : nodeid of the monitored node

Materials constants

The following parameters are Materials constants used in DDLAB.

• Mu: Shear modulus
• NU: Poisson's ratio
• Ec: Dislocation core energy

 Dislocation core radius used for non-singular force calculation

Miscellaneous

• maxconnections : maximum number of segments a node may have

Flow of the code in DDLab

After setting up the initial configuration and other parameters, both DDLab and ParaDiS will follow the same algorithm to simulate dislocation dynamics, as is listed below:

• calculate the force of each node
• calculate the velocity of each node
• calculate the new position of each node
• make necessary topological changes
• repeat (1) to (4) until the maximum step is reached

DDLab just track all nodal positions and plot them. However, to better understand the code structure, two flow charts are presented in this primer: subroutine map (Fig. 2) and function map (Fig. 3). The subroutine map consists of the MATLAB subroutine file name, but the function map consists of the function of each subroutine file. Thus, if you want to know the code in detail, just compare the subroutine map with the function map, then find the file you want and take a look at. Thus, these two maps are very useful to study the code structure of DDLab. All functions of subroutines are explained in the following section which includes some physics for the detailed explanations.

Subroutines details

• SegSegforce.c

This subroutine calculates the force on the two end nodes between two dislocation seg- ments (so, four nodes) in Fig. 4. The sum of these four force vectors should be zero by action-reaction principle. f1 + f2 + f3 + f4 = 0

Figure 4: The interaction between the two dislocation segments

• cleanupnodes.m

This subroutine start by removing all of the bad nodes in the system and cleans up the data structures to include good nodes only. A bad node is a point without connection to any dislocation segment. The point is usually generated by the shrinkage of a dislocation loop as shown in Fig. 5. At the final stage, the loop consists of two nodes, so the line direction of two segments is opposite, but their Burgers vector is the same. Thus, two segments should annihilate. Then, only two nodes remains. These two nodes are only a mathematical points in elastic medium. In real material, the loop disappears after shrinkage, so the two nodes in DDLab has to be removed. Thus, cleanupnodes.m performs the removal of these kinds of isolated nodes.

Note:

This is very similar with to another case (two nodes and two segments) of collision.m. Sometimes segments are not permitted to annihilate when the sum of Burgers vectors are not zero. However, in the case of loop shrinkage, two segments always have the opposite direction of line sense with the same Burgers vector. Thus, the annihilation occurs. See collision.m section.

• genconnectivity.m

This subroutine generates connectivity and linksinconnect. In fact, rn and links matrices are enough to describe the dislocation structure. These two matrices give linkid when we know nodeid. Conversely, connectivity and linksinconnect give nodeid when

Figure 5 The shrinkage of a dislocation loop. we know linkid Here, nodeid is the node number which is the row number of rn matrix. linkid is the link number which is the row number of links matrix.

Integrator

Integrator calls drndt.m, drndt.m computes velocity and force on each node, and force on each segment. Then, by using these values, Integrator integrates the velocity with respect to time step. Then, we can get the nodal positions at the current time step. The nodal forces and the mobility model comprise the equations of motion of nodes:

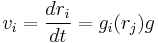
where function g_i sums up both the nodal force and the mobility model. This is first ordinary differential equation (ODE), for which the simplest numerical integrator is the so- called Euler forward method:

r_i(t + Δt) = r_i + g_i(r_j(t))Δt:

A numerical integrator with a higher order of accuracy is the trapezoid method, r_i(t + Δt) = g_i(r_j(t)) + g_i(r_j(t + Δt))

Another important feature of integrator is the time step adjustment. When the time step is large, we can perform simulation which require long physical time. However, the large time step always bring large error. Conversely, when the time step is too short, we can perform the more precise simulation, but it take too long CPU time to get the result. Thus, it is better to adjust the time step in every cycle. The present version of DDLab has the time step adjustment as below. This is the part of the integrator code. ...err = rnvec1 − rnvec0 − (vnvec + vnvec0) / 2 * dt;...errmag = max(abs(err));...if(errmag < rntol)break;elsedt = dt / 2;...maxchange = 1.2;... If the defined err is larger than rntol, the time step is adjusted as the half of current time step. If the defined err is smaller than rntol, the time step is adjusted as 1.2 times of current time step. Thus, DDLab changes its time step dynamically, enabling a much more efficient simulation.

A series of time integration schemes are also included with the distribution named int eulerforward, int eulerbackward, int newtonkrylov. int eulerforward is an explicit forward integration scheme. <tt>int eulerbackward is a simple implicit time integration scheme, and int newtonkylov is a more sophisticated inexact implicit time integration scheme based on the Newton-Krylov matrix-free solution method. The core of the int newtonkrylov employs a method written by C. T. Kelley. The time integration scheme is specified in the input deck with the integrator input parameter.

4.0.14 drndt.m drndt.m calls segforcevec.m. segforcevec.m calculates the force on each segment, then return it to drndt.m. Then, drndt.m calls mobility. mobility calculates the force and velocity on each node and return them to drndt.m Finally, drndt.m return the velocity on node to integrator, which integrate the velocity with respect to time step. Then, we can get the nodal positions at the current time step. 4.0.15 segforcevec.m segforcevec calculates the force on each segment. Note that this is the force not on the node but on the segment. It is because DDLAB use Peach-Koehler formula f_PK(x) = ((x)b)(x) . When we compute PK force, we need to know the line sense vector (�) for segment. Thus, firstly DDLAB calculates the force on each segment which has two end nodes. Then, mobility function gives the half of force to each node. Finally, we can get the nodal force. segforcevec.m includes the four functions; constructsegmentlist, pkforcevec, selfforcevec, remoteforcevec. constructsegmentlist give us the list of all information about segments as the format n0, n1, bx, by, bz, x0, y0, z0, x1, y1, z1, nx, ny, nz, where n0 and n1 are nodeids of two end nodes. bx, by, bz is the Burgers vector of one segment which consists of two end node, n0 and n1. x0, y0, z0 is the position of node n0 and x1, y1, z1 is the position of node n1. nx, ny, nz is the normal vector of the glide plane on which the dislocation segment lies. Based on this list, segforcevec calculate the forces on each segment. selfforcevec calculates the force on each segment by itself. remoteforcevec calculates the force on the segment on each segment by the other segments. Finally, the sum of these forces is the force on segment as below. fseg=[fpk, fpk]*0.5+[fs0, fs1]+[fr0, fr1]; The first component of fseg (fpk, fs0, fr0) are the force vectors on node n0 and the second ones are the force vectors on the node n1. The node n0 and n1 are the end nodes of each segment as shown in Fig. 5.

Figure 7: (a) The example dislocation structure. (b) DDLAB calcuate the force on the segment by segforcevec.m (c) Then, the half of the force is assigned to two end nodes of each segment (d) The force on the node has several arms is just the summation of forces on corresponding arms. 4.0.16 mobfcc1.m, mobfcc0.m, mobfcc1.m A dislocation's response to forces may also depends on the line orientation and varies significantly from one material to another. Similar to the core energy, how dislocation respond to forces is a function of the non-linear atomistic interactions in the dislocation core and, as such, is beyond the scope of linear elasticity theory. The response functions have to be imported into the line DD model in the form of external materials input, either from atomistic simulations or from experiments A series of mobility functions are included in the distribution named mobbcc0 mobbcc0b and mobfcc1. mobbcc0 and mobbcc0b are intended to simulate bcc behavior in which the the screw dislocations are able to glide in any plane normal to their Burgers vector. The difference between them is slight and appears in the mobility of dislocations of mixed character. mobfcc1 is intended to simulate fcc behavior in which the screw dislocation are not able to cross-slip. The mobility function is chosen in the input deck with the mobility input parameter.

4.0.17 separation.m For numerical and physical reasons, line-DD simulations need to handle topological changes, i.e. changes on the connectivity between nodes since we may want to adjust the number of nodes that represent a dislocation line if the line gets longer or shorter during the simulation, or when two dislocation lines meet in space, they may either annihilate or zip together to form a junction, which also results in a change of nodal topology. Thus many types of topological changes can be encountered in a line-DD simulation. Fortunately, since we use a nodal representation here, all topological changes can be implemented through two basic operators: split (one node split into two ) and merge (two nodes merge into one) (See next section) and . The implementation of these two operators is straightforward - all one needs to do is to make sure that at the end of the operation the Burgers vector sum rule at every node and segment is still satisfied, moreover, two nodes are either disconnected or connected only once, and each node is connected with at least two other nodes, if a node has no segment, it will be deleted. For example, for a 4-arm node such as P in there are 3 different ways to partition its arms: (12)(34), (13)(24) and (14)(23). It is reasonable to expect that the way nature would choose should be the one that gives rise to the maximum energy dissipation rate, which is defined below. Suppose an n-arm mode i stays intact (not splitting) and it feels a force fi and will move at velocity vi . Then the local energy dissipation rate is, W_i = f_iv_i. Now suppose that node i splits into two nodes P and Q, such that node P retains 1, ... ,s of the original neighbors, and node Q retains the remaining neighbors. Let fP and fQ be the forces on the two nodes and vP and vQ be their velocities given by the mobility function. Then the local energy dissipation rate is, WP_Q = fPvP + fQvQ.

If WPQ > Wi, then node i prefers to split into two nodes P and Q instead of moving

as a single node. The energy dissipation rate can be computed for all possible (topological distince) modes to split i. The mode with the highest energy dissipation rate is preferred. If a node will split in next step, the two new nodes actually stay at the same location as the parent node at the current step. Because the velocities of the two nodes is different (otherwise the node should not split), the two nodes will be move away from each other in the next time step.

• collision.m

• remesh.m

Self consistency in DDLab units

The unit system of DDLab input file should be self-consistent. We recommend to input all variables in S.I. units.

For instance, stresses in Pascal, distances in meter, times in seconds and velocities in m/s.

The mobility law is such that

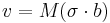
with b in meter, σ in Pascal, and v in m/s. That makes the mobility parameter M in Pa ^{− 1}s ^{− 1}.

We often use the drag coefficient B = M ^{− 1} in the mobility law. The unit of B is

As another option, we can change the unit for distance (including both nodal positions and Burgers vectors) to nm, whereas the unit for stress is still Pa, the unit of time is still second, and the unit for mobility is still Pa ^{− 1}s ^{− 1}.