Test Case: Frank-Read Source

Introduction

Frank-Read source is a type of dislocation multiplication mechanism. Consider a segment whose ends are pinned (corresponding to nodes in a network, precipitates, or sites where the dislocation leaves the glide plane). Under a certain applied stress the segment bows out by glide. As bow-out proceeds, the radius of curvature of the line decreases and the line-tension forces tending to restore the line to a straight configuration increase. For stress less than a critical value, a metastable equilibrium configuration is attained, in which the line-tension force balances that caused by the applied stress. For the large bow-out case, following equilibrium condition holds:

$b\mathbf{\sigma} = \frac{\mathbb{S}}{r}=\frac{\mu b^2}{4\pi r\left( 1-\nu\right)} \left \{ \left [ 1- \frac{\nu}{2} \left ( 3-4 \cos^2\beta \right ) \right ] \mathrm{ln} \frac{L}{\rho} -1 + \frac{\nu}{2} \right \}$

(Hirth-Lothe, p. 752)

where r is the radius of the loop. The radius of the curvature is a minimum when $r = L / 2$ . Hence the maximum stress for which local equilibrium is possible is given by the equation above with $r = L / 2$ . For the typical case that $L = 10 3 ρ$ and $μ = 0.33$ , the critical stress for a dislocation initially pure edge and pure screw, respectively, is $σ * = 0.5μ b / L$ and $σ * = 1.5μ b / L$ .

When the net local resolved shear stress( the applied stress plus the internal stresses) exceeds $σ *$ , the loop has no stable equilibrium configuration but passes through the successive positions. Provided that the expanding loop neither jogs out of the original glide plane because of intersections with other dislocations nor is obstructed from rotating about the pinning point, it will annihilate over a portion of its length, creating a complete closed loop and restoring the original configuration. A sequence of loops then continues to form from the source until sufficient internal stresses are generated for the net resolved shear stress at the source to drop below $σ *$ .

To compare the analytic result with DDLab simulation, we need to use the relation $ρ = r c / 2$ . According to the non-singular continuum theory of dislocation (JMPS 54, 561-587, 2006), the energy of a circular prismatic dislocation loop is

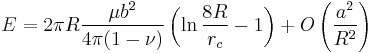
$E = 2 \pi R \frac{\mu b^2}{4 \pi (1-\nu)} \left( \ln \frac{8 R}{r_c} - 1 \right) + O\left(\frac{a^2}{R^2}\right)$

According to Hirth and Lothe, the energy of the same loop is,

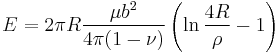
$E = 2 \pi R \frac{\mu b^2}{4 \pi (1-\nu)} \left( \ln \frac{4 R}{\rho} - 1 \right)$

Therefore 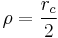$\rho = \frac{r_c}{2}$

Reference: J. P. Hirth and J. Lothe, Theory of Dislocations", 2nd ed. (Wiley, New York, 1982)

DDLab Input Parameter

DDLab has included a Frank-Read Source input file in its latest version 2007-12-28 at ~/Inputs/input_frank_read.m. Following is a brief introduction to some parameters important in Frank-Read source test.

rn--it gives the initial coordinations of nodes. The default setting is a straight dislocation line pinned at (1200,1200,1200) and (-1200,-1200,-1200) with a mobile node in the middle, (0,0,0);

links--a data structure which gives the information of dislocation segment connectivity, burgers vecotors and glide planes;

totalsteps--number of cycles that are run for completion of dd3d command;

appliedstress--external applied stress in the form of 3*3 symmetric tensor;

a--dislocation core radius used for non-singular force calculation, sometimes written as $r c$ .

plotfreq--number of cycles between monitered node write statements, higher number makes observation simpler

We can manipulate these parameters to investigate Frank-Read Sources via DDLab.

F-R Test

It is pretty tricky to determine the critical applied stress to generate a Frank-Read source. When the critical stress is exceeded, the bowing process will never stop. We can guess an initial value anyway, and run for certain number of steps to see if dislocation has grown to a critical configuration. I would prefer the maximum distance criteria, that is, we can extract the coordinations of all nodes from rn and compare the their maximum distance perpendicular to initial straight dislocation line with an empirical value. If the maximum distance is less than that value, a little higher external stress will be applied and run the DD simulation again. When the critical stress is reached, the bow will keep going, even farther away as long as enough time steps are run. After several trials, it proves safe to set the critical distance as the length of initial dislocation line, i.e. L. For the case 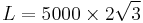$L=5000\times 2\sqrt{3}$ , running 200 steps for each given stress will work perfectly.